Boat & stream
Concept
Boat and Stream is the one of the most crucial methods of testing aptitude. In competitive exams this type of math is provided as brain teaser. The concept of this type of math is basically based on different conditions of stream such as still water, downstream & upstream and speed of boat. For further proceed we need to know these terminologies those are defined below:
- Stream – The water flowing in any direction in a river or creek is called a stream.
- Upstream – If the boat is flowing against the stream, it is called upstream. In this case, the net speed of the boat is called the upstream speed
- Downstream – If the boat is flowing along the stream, it is called downstream. In this case, the net speed of the boat is called downstream speed
- Still Water – Under this circumstance the water is considered to be stagnant and the speed of the water is zero.
- Boat Speed – The velocity at which the boat is running in still water.
Tips to solve problem on Boat & Stream:
- If the boat goes Upstream, actual speed = Speed of Boat – Speed of Current
- If the boat goes Downstream, actual speed = Speed of Boat + Speed of Current
- Speed of Boat in Still Water = ½ (Downstream Speed + Upstream Speed)
- Speed of Stream = ½ (Downstream Speed – Upstream Speed)
- Average Speed of Boat = [(Upstream Speed × Downstream Speed) / Boat’s Speed in Stii Water]
- Distance Covered =Actual Speed of the Boat x Time Spent
Q. A boat can travel 20 miles downstream in 2 hours. The return trip against the current takes 5 hours. What is the speed of the boat in still water, and what is the speed of the current ?
A) 12 mph & 10 mph
B) 5 mph & 8 mph
C) 10 mph & 5 mph
To solve this problem, we can use the formula: Speed = Distance / Time. Let’s denote the speed of the boat in still water as B and the speed of the current as C. From the given information, we have two equations:
• 20 = (B + C) * 2 (downstream trip)
• 20 = (B - C) * 5 (return trip) Solving these equations simultaneously, we find that B = 10 mph and C = 5 mph.
D) 10 mph & 14 mph
Discuss
Q. A fisherman rows a boat for 8 km at 8 km/hr at downstream for setting his net and returns to starting point at 2 km/hr. What is the speed of boat in still water?
A) 3 km/hr
B) 5 km/hr
We know, Speed at downstream=Speed of Boat + Speed of Current and Speed at Upstream=Speed of Boat – Speed of Current. By adding up the equations we get, 2 Speed of Boat=8+2 Or, Speed of Boat=5 km/hr.
C) 2.5 km/hr
D) 4 km/hr
Discuss
Q. Speed of a boat in still water is 6 km/hr. When the river is running at 2.50 km/hr, it takes the boat 2 hours to row to a destination and back to the starting point. What is the distance between the places?
A) 3.50 km
B) 5.00 km
Here, speed at downstream  =8.5km/hr & speed at upstream
=8.5km/hr & speed at upstream  =3.5km/hr. We know, Time=
=3.5km/hr. We know, Time= . Now, let distance=x km. According to question, Total time=Time taken for destination+Time taken for return=2 Or,
. Now, let distance=x km. According to question, Total time=Time taken for destination+Time taken for return=2 Or,  =2 Or,
=2 Or,  =119 Or,
=119 Or,  =119 Or,x=
=119 Or,x= =5.00
=5.00
C) 5.25 km
D) 7.00 km
Discuss
Q. In a stream, running at 2 km/hr, a motor boat goes point A and return to point B after 10 minutes later. The whole journey took one hour 5 minutes. What is the distance from point A to B if the speed of the boat in still water is 22 km/hr.
A) 10 km
Let, distance= x km. We know, Time=Distance/Speed. So, Time at downstream= hr. & Time at upstream=
hr. & Time at upstream= hr. According to question,
hr. According to question,  hr. Or,
hr. Or,  Or,
Or,  Or, x=
Or, x= km.
km.
B) 12 km
C) 16 km
D) 18 km
Discuss
Q. A tugboat takes 4 hours for going to doc at downstream for engine servicing from a terminal of 6 km distance and return to the terminal at upstream. If speed of the tugboat at still water is four kilometer, what will be the velocity of stream?
A) 4 km/hr
B) 2 km/hr
Let, velocity of stream = km/hr. So, speed of the tugboat at downstream=
km/hr. So, speed of the tugboat at downstream= km/hr and speed at upstream=
km/hr and speed at upstream=  km/hr. We know, Time=Distance/Speed. According to question,
km/hr. We know, Time=Distance/Speed. According to question,  Or,
Or,  Or,
Or,  Or, x=
Or, x= .
.
C) 6 km/hr
D) 5 km/hr
Discuss
Q. A man can row 30 km upstream and 44 km downstream in 10 hours. Again, he can row 40 km upstream and 55 km downstream in 13 hours. If he goes 48 km and return to starting point without delay, what time he will be needed?
A) 16 hr
B) 21 hr
C) 14 hr
Let, Speed at upstream= km/hr and Speed at Downstream=
km/hr and Speed at Downstream= km/hr. So,
km/hr. So,  ----------(I) &
----------(I) &  -------------(II). Now, solving the equation (I) & (II) we get,
-------------(II). Now, solving the equation (I) & (II) we get, 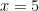 and
and  . Therefore total time required for
. Therefore total time required for  hours =
hours =  hours.
hours.
D) 12 hr
Discuss

